你好旅行者!欢迎来到cyt的练功房。本篇文章来记录一下力扣的第328场周赛
一、数组元素和与数字和的绝对差
题目:
给你一个正整数数组 nums 。
- 元素和 是 nums 中的所有元素相加求和。
- 数字和 是 nums 中每一个元素的每一数位(重复数位需多次求和)相加求和。
返回 元素和 与 数字和 的绝对差。
注意:两个整数 x 和 y 的绝对差定义为 |x - y| 。
输入:nums = [1,15,6,3]
输出:9
解法:
很简单的一道题,就是总的和加上每个数字的和。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
int differenceOfSum(vector<int>& nums) {
int nums1=0,nums2=0;
for(int i=0;i<nums.size();i++){
nums1+=nums[i];
while(nums[i]){
nums2+=nums[i]%10;
nums[i]/=10;
}
}
return abs(nums1-nums2);
}
};
|
二、子矩阵元素加 1
题目:
给你一个正整数 n ,表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ,矩阵中填满了 0 。
另给你一个二维整数数组 query 。针对每个查询 query[i] = [row1i, col1i, row2i, col2i] ,请你执行下述操作:
找出 左上角 为(row1i, col1i) 且 右下角 为 (row2i, col2i) 的子矩阵,将子矩阵中的 每个元素 加 1 。也就是给所有满足 row1i <= x <= row2i 和 col1i <= y <= col2i 的 **mat[x][y]**加 1 。
返回执行完所有操作后得到的矩阵 mat 。
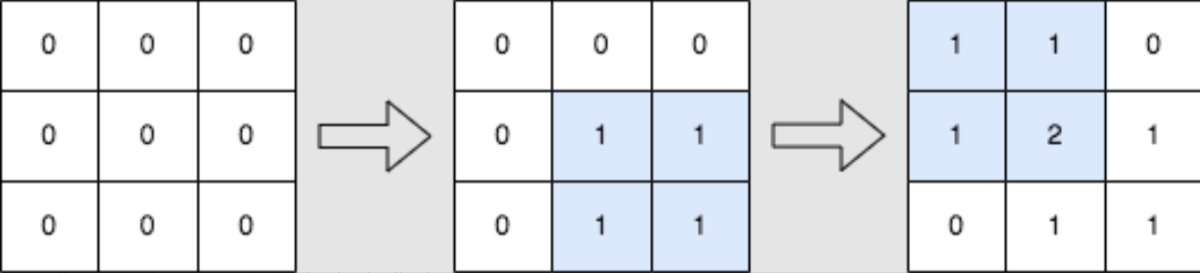
解法:
二维差分模板题,建议直接使用模板进行差分的构建,构建完之后求个前缀和就行了,唯一要注意的是在构建差分数组时数组要多开一个,wa了一次
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
vector<vector<int>> rangeAddQueries(int n, vector<vector<int>> &queries) {
vector<vector<int>> mat(n, vector<int>(n, 0));
vector<vector<int>> diff(n+1, vector<int>(n+1, 0));
for (int k = 0; k < queries.size(); k++) {
int x1 = queries[k][0];
int y1 = queries[k][1];
int x2 = queries[k][2];
int y2 = queries[k][3];
diff[x1][y1]++;
diff[x2+1][y1]--;
diff[x2+1][y2+1]++;
diff[x1][y2+1]--;
}
for(int i = 0; i < n; ++i){
for(int j = 0; j < n; ++j){
if(i > 0) diff[i][j] += diff[i - 1][j];
if(j > 0) diff[i][j] += diff[i][j - 1];
if(i > 0 && j > 0) diff[i][j] -= diff[i - 1][j - 1];
}
}
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
mat[i][j]=diff[i][j];
}
}
return mat;
}
};
|
三、统计好子数组的数目
题目:
给你一个整数数组 nums 和一个整数 k ,请你返回 nums 中 好 子数组的数目。
一个子数组 arr 如果有 至少 k 对下标 (i, j) 满足 i < j 且 arr[i] == arr[j] ,那么称它是一个 好 子数组。
子数组 是原数组中一段连续 非空 的元素序列。
解法:
子数组是一个连续的过程,思考大致为双指针算法仔细一思考确实是当j确定时,i单调向前进,所以可以用双指针来做。
定义[i,j]用hash表存储[i,j]中每个数出现的次数,res为出现的对数,hash[c]每多出现一次,res就增加hash[c]-1;
首先移动j,当j移动到某一个res>=k时ans++,(此时不能是ans+=(nums.size()-j),因为j会继续移动导致重复计算),在res>=k时,移动i,i每次向右移动一个判定是否成立,若成立,则ans+=(nums.size()-j),这个不会重复。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
long long countGood(vector<int>& nums, int k) {
long long i=0,j=1,res=0,ans=0;
unordered_map<int,long long> hash;
hash[nums[0]]++;
while(j<nums.size()){
hash[nums[j]]++;
if(hash[nums[j]]>1)res+=(hash[nums[j]]-1);
if(res>=k){
ans+=1;
}
while(i<j){
res-=(hash[nums[i]]-1);
if(res>=k){
ans+=(nums.size()-j);
hash[nums[i++]]--;
}
else{
res+=(hash[nums[i]]-1);
break;
}
}
j++;
}
return ans;
}
};
|
四、最大价值和与最小价值和的差值
根本做不出来,感觉应该是树形dp,写出来超时,看了题解也不知道为啥错
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
long ans=0;
pair<long,long> dp(int x,int fa,vector<vector<int>> tu,vector<int> price){
long max_s1=price[x],temp=price[x];
long max_s2=0;
pair<long,long> p;
for(auto y:tu[x]){
if(y==fa)continue;
auto[s1, s2] = dp(y, x,tu,price);
ans=max(ans, max(max_s1 + s2, max_s2 + s1));
max_s1=max(max_s1,s1+temp);
max_s2=max(max_s2,s2+temp);
}
return {max_s1,max_s2};
}
long long maxOutput(int n, vector<vector<int>>& edges, vector<int>& price) {
vector<vector<int>> tu(n);
for(auto x:edges){
tu[x[0]].push_back(x[1]);
tu[x[1]].push_back(x[0]);
}
dp(0,0,tu,price);
return ans;
}
};
|
